un árbol es una estructura de datos ampliamente usada que imita la forma de un árbol (un conjunto de nodos conectados). Un nodo es la unidad sobre la que se construye el árbol y puede tener cero o más nodos hijos conectados a él. Se dice que un nodo a es padre de un nodo b si existe un enlace desde a hasta b (en ese caso, también decimos que b es hijo de a). Sólo puede haber un único nodo sin padres, que llamaremos raíz. Un nodo que no tiene hijos se conoce como hoja. Los demás nodos (tienen padre y uno o varios hijos) se les conoce como rama.
Operaciones de árboles.
RepresentaciónLas operaciones comunes en árboles son:
--Enumerar todos los elementos.
--Buscar un elemento.
--Dado un nodo, listar los hijos (si los hay).
--Borrar un elemento.
--Eliminar un subárbol (algunas veces llamada podar).
--Añadir un subárbol (algunas veces llamada injertar).
--Encontrar la raíz de cualquier nodo.
--Por su parte, la representación puede realizarse de diferentes formas. Las más utilizadas son:
----Representar cada nodo como una variable en el heap, con punteros a sus hijos y a su padre.
----Representar el árbol con un array donde cada elemento es un nodo y las relaciones padre-hijo vienen dadas por la posición del nodo en el array.
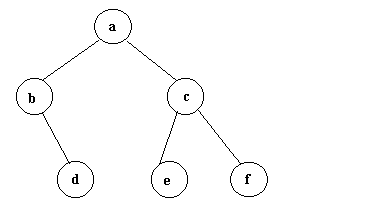 |
| Figura 1 |
- Recorridos en profundidad:
Si se hace el recorrido en preorden del árbol de la figura 1 las visitas serían en el orden siguiente: a,b,d,c,e,f.
* Recorrido en inorden u orden central: se visita el subárbol izquierdo, el nodo actual, y después se visita el subárbol derecho. En el ejemplo de la figura 1 las visitas serían en este orden: b,d,a,e,c,f.
* Recorrido en postorden: se visitan primero el subárbol izquierdo, después el subárbol derecho, y por último el nodo actual. En el ejemplo de la figura 1 el recorrido quedaría así: d,b,e,f,c,a.